Understanding The Constant Of Proportionality In Direct Variation

Insurance

In mathematics, direct variation is a fundamental concept that involves relationships between variables. When two variables exhibit direct variation, they change at a constant rate relative to each other. This constant relationship is expressed through the constant of proportionality, which plays a crucial role in understanding how one variable affects the other. The constant of proportionality is a key element in equations that describe direct variation, typically represented as 'k' in the equation y = kx. Grasping this concept is essential for students and professionals alike, as it appears in various fields such as physics, economics, and engineering.

The constant of proportionality gives us insight into the strength and nature of the relationship between the two variables involved. When we say that y varies directly with x, it means that as x increases, y increases proportionally, and similarly for decreases. This relationship allows us to predict values and understand how changes in one variable will affect the other. Therefore, determining the constant of proportionality is not just an academic exercise; it has practical applications in real-world scenarios.

In this article, we will explore the concept of the constant of proportionality in direct variation in detail. We will answer questions such as what it is, how to find it, and why it is important. Whether you are a student aiming to master this topic or someone looking to refresh your knowledge, this comprehensive guide will shed light on the constant of proportionality and its significance in direct variation.

What is Direct Variation?

Direct variation is a mathematical relationship where two variables change in a consistent manner. When one variable increases, the other does as well, and they do so at a constant ratio. This can be expressed mathematically as:

y = kx

Where 'y' and 'x' are the variables involved, and 'k' is the constant of proportionality. This equation indicates that for every unit increase in x, y increases by 'k' units.

How Do You Find the Constant of Proportionality?

Finding the constant of proportionality is straightforward if you have values for both variables. Here’s how you can determine 'k':

  • Identify the values of x and y from the direct variation equation.
  • Divide the value of y by the value of x.
  • The quotient is the constant of proportionality (k).

    • For example, if y = 12 when x = 3, then:

    k = y/x = 12/3 = 4

    This indicates that the constant of proportionality is 4.

    Why is the Constant of Proportionality Important?

    The constant of proportionality is vital for several reasons:

    • It allows for predictions: Knowing the constant of proportionality helps in forecasting values of one variable based on another.
    • It simplifies calculations: Understanding the relationship between variables can make complex problems more manageable.
    • It applies to real-world situations: From economics to physics, the constant of proportionality can be observed in various phenomena.

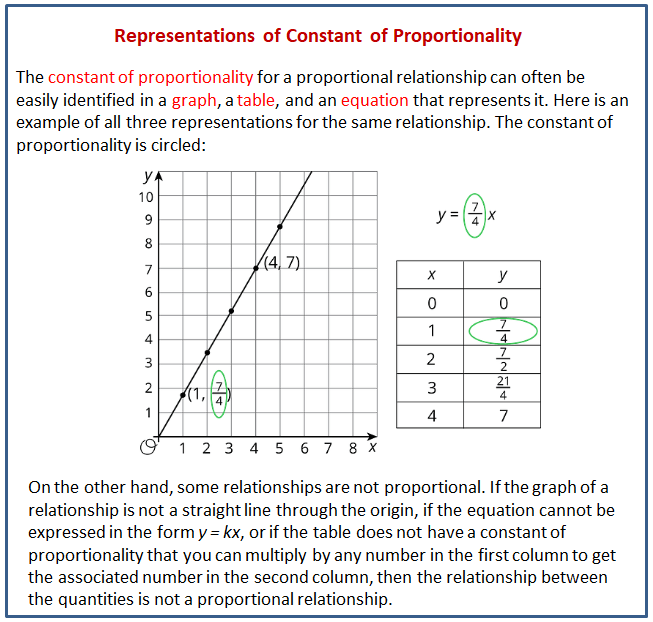
    What is the Constant of Proportionality in This Direct Variation?

    To reiterate, the constant of proportionality in a direct variation equation y = kx is represented by 'k'. It reflects how much y changes for a given change in x. Understanding this constant can provide deeper insights into the nature of the relationship between the variables involved.

    Examples of Direct Variation

    Let’s explore a few examples to illustrate the concept of direct variation and the constant of proportionality:

    • Example 1: If the number of apples (y) is directly proportional to the number of baskets (x) used to collect them, and you find that 10 apples are collected in 2 baskets. Here, k = 10/2 = 5, meaning each basket contains 5 apples.
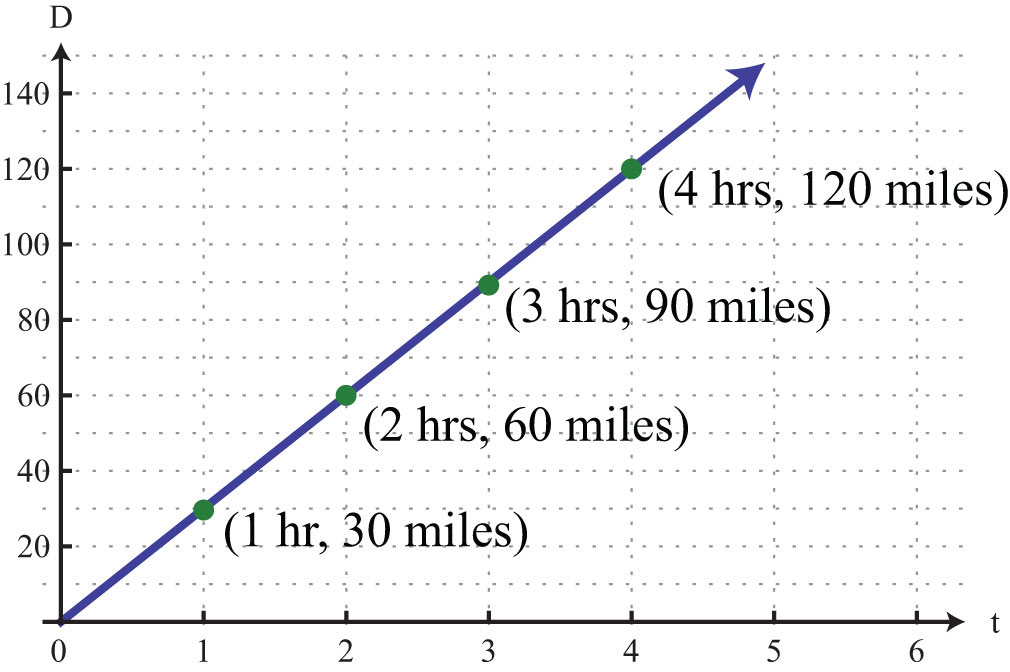
    • Example 2: If a car travels at a constant speed, the distance (y) it covers is directly proportional to the time (x) it travels. If it covers 120 miles in 2 hours, then k = 120/2 = 60 miles per hour.

    How Does the Constant of Proportionality Relate to Graphs?

    The constant of proportionality can also be observed in graphing the relationship between two variables. In a graph of direct variation:

    • The line passes through the origin (0,0).
    • The slope of the line represents the constant of proportionality (k).

    This means that if you were to plot the points corresponding to the variations, the steeper the line, the larger the constant of proportionality. A horizontal line indicates no variation, while a vertical line is undefined.

    What Are Some Common Misconceptions About the Constant of Proportionality?

    Understanding the constant of proportionality can be challenging, and several misconceptions can arise:

    • Some may think that any relationship between two variables is a direct variation, but that is not the case. Only relationships that maintain a constant ratio qualify as direct variation.
    • Another misconception is that the constant of proportionality can be negative. While it can be, it simply indicates an inverse relationship, which does not fall under direct variation.

    Conclusion: What is the Constant of Proportionality in This Direct Variation?

    Understanding the constant of proportionality in direct variation is essential for grasping the dynamics between variables in mathematics and real-life applications. By identifying the constant 'k', one can predict outcomes, simplify calculations, and comprehend the nature of relationships in various fields. As we've explored in this article, recognizing how to find and interpret the constant of proportionality is a crucial skill that can enhance your mathematical proficiency and problem-solving capabilities. Whether you are a student or a professional, mastering this concept can empower you to approach mathematical challenges with confidence and clarity.




    ncG1vNJzZmixn6PAtr7IZqWeq6RjsLC5jq2pnqaUnruogY6wn5qsXZ7AbsDHnmScp56owaK602amn2Wgp7yxu9GtoKimkaG2tcWMoqVmrJiewG6wyKucnKxdq66ztcCtoKimXp3Brrg%3D